To calculate a worm gear with center distance 100 mm. The worm has 2 teeth, and the worm wheel has 41 teeth. The axial/transverse module is 4. The pressure angle at the normal section is 20°. The worm's facewidth is 60 mm. You should select a sensible facewidth for the worm wheel. The axis tolerance is js7.
ZAR3+ generates true-scale drawing of worm and worm gear. ZAR3+ provides an additional input window for modifications of tooth height factors and profile shift coefficient x. These functions are useful for design of complementary gears of steel worm and plastic worm gear. ZAR3+ calculates tooth thickness and over pin/ball diameters (OPD). Worm Gears Common to specify lead angle lfor worm and helix angle G for gear. Common to specify axial pitch p x for worm and transverse circular pitch p t for gear. Pitch diameter of gear is measured on plane containing worm axis Shigley’s Mechanical Engineering Design Fig. Load calculation of gears 239 11.5 Calculation of load on worm gear A worm gear is a kind of spigot gear, which can produce a high reduction ratio with small volume. The load at a meshing point of worm gears is calculated as shown in Table 1. Symbols of Table 1 are as follows: i: Gear ratio i= 1 = ´ gear) 11.1, Calculation of loads on spur. Worm Gear Design Pdf; Worm Gear Calculation; Worm Gear Design Excel; Worm Gear Design Guide; Worm Gear Design Calculation; Worm Gear Manual Gears and linear products since 1964 /// Page 2 Design of the worm gear /// Page 3 Mounting instructions /// Page 4 Operating instructions and choice of oil /// Page 5 Unique gear number /// Page 6 Spare parts diagram /// Page 7 Spare parts list /// Page 8. Gear Design National Broach and Machine Division,of Lear Siegler, Inc. A gear can be defined as a toothed wheel which, when meshed with another toothed wheel with similar configura-tion, will transmit rotation from one shaft to another. Depending upon the type and accuracy of motion desired, the gears and the profiles of the gear teeth can be.
ZAR3 Worm Gear Calculation ZAR3+ Software for Cylindrical Worm Gear Design (C) Copyright 1993-2017 by HEXAGON Software, Berlin Bases for Calculation ZAR3 calculates all dimensions of cylindrical worm gear pairs with ZI, ZA, ZK, ZN or ZH worms, as well as efficiency, tooth forces and the safety margins against root fatigue fracture and pitting. Pre-dimensioning In pre-dimensioning recommendations are made for axial distance, modulus and number of teeth based on gear ratio, drive power, drive rotational speed and material. The recommendations can be used in the following geometry and strength calculations. Geometry Calculation In dimensioning you can adjust the recommended values to match available sizes or company standards. Or by varying the axial distance ratio and addendum modification you can determine the optimum worm gear for your application.
Strength Calculation The strength calculation computes the factors SF (fatigue fracture) and SH (pitting) along with tooth forces on the worm and worm gear, as well as the efficiency of the gear. Efficiency ZAR3 calculates the toothing efficiency, toothing and idling loss of power. The program provides recommended values and help graphics for determination of the tooth friction value. Material Data Base The program already includes a data base containing the most important gear materials and their values.
Users of the ZAR1+ spur gear and ZAR2 bevel gear programs can access this as a common data base. Tooth Forces Axial and radial forces, as well as tangential force and normal force are calculated. These values can be transfered to the WL1/WL1+ software for shaft calculation. Plus-Version ZAR3+ The extended version ZAR3+ provides additional functions: ZAR3+ generates true-scale drawing of worm and worm gear.
ZAR3+ provides an additional input window for modifications of tooth height factors and profile shift coefficient x. These functions are useful for design of complementary gears of steel worm and plastic worm gear. ZAR3+ calculates tooth thickness and over pin/ball diameters (OPD). You can enter pin diameter and flank tolerances or select from tolerance system according to DIN 3967.
CAD Interface A true-scale drawing of worm and worm wheel, as well as tables with the gear data can be exported to CAD via the DXF or IGES interfaces. The drawings can of course also be displayed on screen and printed out. Import/Export Text printout can be generated as HTML table and exported to Excel. Input data may be loaded from an Excel worksheet.
HEXAGON Help System For all entries a help text or auxiliary picture can be displayed. For example, there are diagrams for input of the tooth friction value µz0 in relation to lubricant and average slide speed. There are also diagrams for optimizing the diameter-to-center distance ratio dm1/a in relation to fatigue stress or efficiency. Users can modify and append help texts and auxiliary pictures. When error messages occur you can have an error description and remedy suggestion displayed.
Hardware and Software Requirements ZAR3+ is available as 32 bit and 64 bit application for Windows 7, Windows 8, Windows 10. Scope of Delivery CD-ROM or zip file for download with program and pdf manual, License agreement for indefinite period of time. Information and Update Service HEXAGON Software is continuously improved and updated. Licensed users can obtain new versions at the update price.
Worm Gear Design Calculation Pdf Files Pdf
Each program is provided with an individual license number and user files. No extra charge is made to registered users for telephonic support and hotline use.
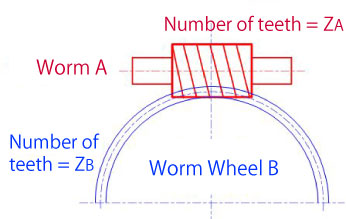
A worm gear box must contain a worm and a mating gear (helical gear) and normally the axis of the worm is perpendicular to the axis of the gear. Look at the picture below:
Where,
Calculations for worm gears are the same as for. Worm Gearing 50 Lead Angle Worm threads are. Perature and the details of the gear mesh design. Worm gear.pdf - Free download as PDF File (.pdf), Text File (.txt) or read. Of a worm gear is related to its circular pitch and number of teeth Z by the formula.
D1 – Pitch Diameter of Worm
D2 – Pitch Diameter of Gear
C – Centre to Centre Distance between the Worm and the Gear
This worm gear design tutorial will discuss up to the selection of the module and pitch and the calculation of the number of teeth, pitch circle diameter and centre to centre distance between the worm and gear. We will use the AGMA formulae for doing the calculations. Design calculations of the other aspects of the worm gear will be discussed in a subsequent part of the tutorial.
Steps of the Design Calculation
- The axial pitch of the worm and the circular pitch of the gear must be same for a mating worm and gear. We will use the term Pitch (P) for both the pitch in this tutorial.
- Also, the module of the worm as well as the gear must be equal for a mating worm and gear.
- Now, let’s say we have the following design input:
Speed of the Worm (N1) = 20 RPM
Free Worm Gear Calculator
Speed of the Gear (N2) = 4 RPM
- And, we have to find out the Module (m), Pitch (P), Number of helix of Worm (T1), Number of teeth of Gear (T2), Pitch circle diameter of Worm (D1), Pitch circle diameter of Gear (D2), Centre to centre distance(C).
- Select the suitable module and its corresponding pitch from the following AGMA specified table:
Module m (in MM) – Pitch P (in MM)
2 ————————-6.238
Worm Gear Calculation
2.5 ———————- 7.854
3.15 ——————— 9.896
4 ————————- 12.566
5 ————————- 15.708
6.3 ———————– 19.792
8 ————————– 25.133
10 ————————- 31.416
12.5 ———————– 39.27
16 ————————– 50.625
20 ————————– 62.832
- Say, we are going ahead with the Module as 2 and the Pitch as 6.238.
- Use the following gear design equation:
N1/N2 = T2/T1
And, we will get:
T2 = 5 * T1……………….Eqn.1
- Now use the following AGMA empirical formula:
T1 + T2 > 40………………Eqn.2
- By using the two equations (Eqn.1 & Eqn.2), we will get the approximate values of
T1 = 7 andT2 = 35
- Calculate the pitch circle diameter of the worm (D1) by using the below AGMA empirical formula:
D1 = 2.4 P + 1.1
= 16.0712 mm
- The following AGMA empirical formula to be used for calculating the pitch circle diameter of the gear (D2):
D2 = T2*P/3.14
= 69.53185 mm
- Now, we can calculate the centre to centre distance (C) by the following equation:
C = (D1 + D2)/2
= 42.80152 mm
- The below empirical formula is the cross check for the correctness of the whole design calculation:
(C^0.875)/2 <= D1 <= (C^0.875)/1.07
Observe that our D1 value is falling in the range.
Conclusion
The worm gear box design calculation explained here uses the AGMA empirical formulas. A few worm gear design calculator are available on web, and some of them are free as well.
In the next worm gear box design calculation tutorial we will discuss the force analysis of a worm gear box.
Related Reading
Helical Gear vs. Spur Gear: If you have observed a spur gear application, you may have noticed that spur gear can be replaced by helical gear. Where should a helical gear should be used? What are the benefits and disadvantages of doing so?
Input Parameters
Teeth type - common or spiral
Gear ratio and tooth numbers
Pressure angle (the angle of tool profile) α
How to run bully scholarship edition in windowed mode. Then I downloaded one of the best mods called 'Super Mod', and it was still running normally. Only thing I can hope for is Bully 2 or Bully remake in the future. Well, just some pirace games of Bully works for Windows 10, but Rockstar make this game to Rest in Peace. At first crashes but then the game was normal. But now the game crashes frequently.
Module m (With ANSI - English units, enter tooth pitch p = π m)
Unit addendum ha*
Unit clearance c*
Unit dedendum fillet rf*
Face widths b1, b2
Unit worm gear correction x
Worm size can be specified using the:
- worm diameter factor q
- helix direction γ
- pitch diameter d1
Calculated parameters
Common gearing ZN
mn = m | |
Normal module | mx = mn cos γ |
Axial pressure angle | αx = a |
Normal pressure angle | αn = arctg (tg α cos γ) |
Helix/lead angle | γ = arcsin z1/q |
Spiral gearing ZA
mn = mx / cos γ | |
Normal module | mx = m |
Axial pressure angle | αn = arctg (tg α cos γ) |
Normal pressure angle | αx = α |
Helix/lead angle | γ = arctan z1/q The configuration details for this step can be found in the installation guide. |
Normal tooth pitch
Axial tooth pitch
Basic tooth pitch
Lead
Virtual/alternate number of teeth
Helix angle at basic cylinder
Worm pitch cylinder diameter
Worm gear pitch circle diameter
Worm Gear Design Formula
Worm outside cylinder diameter
Worm gear outside circle diameter
Worm root cylinder diameter
Worm gear root circle diameter
Worm rolling(work) circle diameter
Worm gear rolling(work) circle diameter
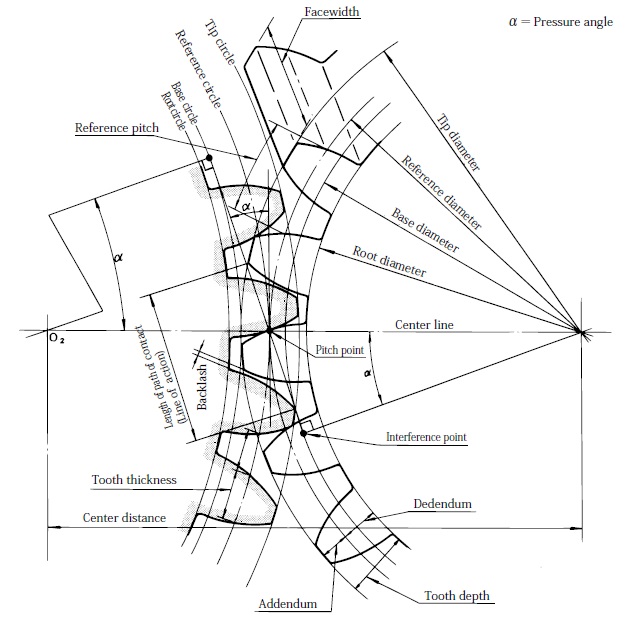
Worm gear root circle diameter
Center distance
Chamfer angle of worm gear rim
Worm tooth thickness in normal plane
Worm gear tooth thickness in normal plane
Worm tooth thickness in axis plane
Worm gear tooth thickness in axis plane
Work face width
Contact ratio
εγ = εα + εβ
where:
Minimum worm gear tooth correction
where:
c = 0.3 | for α = 20 degrees |
c = 0.2 | for α = 15 degrees |
